Prepričani tekst zadatka
Dat je prost neusmeren graf sa N čvorova i M grana. Svaka grana ima težinu koja je prirodan broj, t[i] <= 10. Potrebno je naći broj puteva čija je dužina ne više od K i deljiva je sa D. Dva puta su različita ukoliko im se razlikuje niz čvorova. Jedan put mora sadržati bar dva čvora. Dozvoljeno je ponavljanje čvorova/grana na putu. Put može počinjati ili završavati se u proizvoljnim čvorovima. Broj puteva naći po modulu 10^9 + 7.
Ograničenja:
Ostali podzadaci su olakšane verzije jednog od naredna dva podzadatka.
U jednom podzadatku N <= 80, D, K <= 10000
U drugom podzadatku N <= 30, D, K <= 10^9
Broj grana je jedino ograničen brojem čvorova i uslovom da je graf prost, tj. ne postoji više grana između dva ista čvora i ne postoje grane od jednog čvora do njega samog.
Rešenje 1 - dinamičko programiranje.
Neka je d[l][u][v] broj puteva od čvora u do čvora v čija je dužina tačno l. Rekurentna veza je:
d[l][u][v] = Suma { w : susedi od (v) } d[ l - len[w][v] ][u][w]
d[0][v][v] = 1
d[0][u][v] = 0 za u != v.
Nakon što ove vrednosti izračunamo za sve u, v od 1 do N i za sve l od 1 do K, samo pročitamo zbir svuda gde je l deljivo sa D.
Složenost ovog rešenja je O(n^3 D). Ovo rešava neke podzadatke ali nažalost ne sve.
Rešenje 2 - optimizovano dinamičko.
Kako nam polazni čvor u ne učestvuje u rekurentnoj vezi, možemo da probamo da reformulišemo stanje DP-a i rekurentnu vezu.
Neka je sada dp[l][v] broj puteva dužine l koji se završavaju u čvoru v. Rekurentna veza je:
d[l][v] = Suma { w : susedi od (v) } d[ l - len[w][v] ][w]
d[0][v] = 1
Složenost ovog rešenja je O(n^2 D) što je dovoljno efikasno za podzadatak gde je D relativno mali broj, do 10000.
“2n, n+1” trik
Osvrnimo se na klasičan problem koji je verovatno poznat iskusnijim takmičarima: Naći broj puteva dužine tačno D u grafu, gde sve grane imaju dužinu 1.
Za čitaoce koji barataju jezikom linearne algebre: Ovo se može rešiti stepenovanjem matrice susedstva na D-ti stepen, čije se u polju (A^D)[i][j] dobija broj puteva dužine D od čvora i do čvora j. Stepen matrice može se naći u složenosti O(log D) algoritmom pod nazivom binarno stepenovanje. Ovaj trik se može izvesti i u drugim zadacima dinamičkog programiranja i neformalno se naziva “2n, n+1” trik.
Ideja je sledeća: Ako imamo matricu d[l], mi možemo efikasno naći matricu d[2l], na sledeći način, ukoliko su dužine svih grana 1:
d[2l][u][v] = suma { w : od 1 do n } d[l][u][w] * d[l][w][v]
“Isečemo” put dužine 2l na dva puta dužine l, iteriramo po svim mogućim čvorovima w koji se nalaze na sredini tog puta.
Slično možemo naći i matricu d[l+1] ako znamo matrice d[l] i d[1].
d[l+1][u][v] = suma { w : od 1 do n } d[l][u][w] * d[1][w][v]
Ako želimo da izračunamo K-ti stepen neke matrice, iz binarnog zapisa broja K možemo zaključiti kojim redosledom treba vrštii operacije “2n” i “n+1”.
Vratimo se sada na originalni zadatak. Svaku granu dužine t menjamo sa 2t-2 dodatna čvora i 2t usmerenih grana dužine 1, kao na slici:
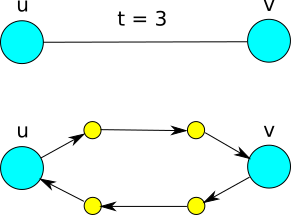
Ovime želimo da eliminišemo problem što je dužina grana veća od 1. Broj čvorova sada može biti ne više od N + 2 * M * (Tmax - 1). Sada pri računanju uzimamo u obzir samo one puteve koji počinju i završavaju se u nekom od originalnih čvorova, a ne nekom od dodatih.
Međutim ovo i dalje ne rešava zadatak. Potrebno je da nađemo sve puteve čija je dužina manja ili jednaka K a deljiva sa D. Uzmimo radi jednostavnosti da D deli K. U suprotnom samo postavimo K = (K div D) * D. Jasno je da ovaj broj možemo naći iz matrice A^D + A^(2D) + A^(3D) + … + A(K/D)D.
Prvo, nađimo D-ti stepen matrice A. Nazovimo tu matricu B. Zatim treba naći B + B^2 + … + B^(K/D). Ovo možemo naći postupkom sličnim binarnom stepenovanju: Pamtimo u svakom trenutku zbir S = B + B^2 + … + B^x i vrednost B^x za neki ceo broj x. Korak “2n” možemo realizovati na sledeći način:
S[2x] = S * B^x + S
B^2x = B^x * B^x
Korak “n+1” možemo realizovati kao:
S[x+1] = S * B + B
B^(x+1) = B^x * B
Ovo rešenje ima složenost O((N + M * Tmax)^3 * log(K)) i radi na podzadacima gde je zbir dužina svih grana mali. (Podzadaci 3 i 4, videti originalni tekst zadatka).
Da bismo rešili zadatak za maksimalan broj poena neophodno je da redefinišemo matricu koju stepenujemo.
Naime, nećemo dodavati nove čvorove. već ćemo dužine grana inkorporirati direktno u matricu (tj. stanje), na sledeći način.
Rešenje za maksimalni broj poena
Vratimo se na polaznu DP jednačinu:
d[l][u][v] = Suma { w : susedi od (v) } d[ l - len[w][v] ][u][w]
Umesto da nam indeksi redova i kolona budu čvorovi, neka to bude par (u, x), gde je u čvor a x broj od 0 do Tmax-1, koliko smo udaljeni od tog čvora duž neke grane, gde pretpostavljamo da se krećemo ka tom čvoru.
Definišemo matricu d[1] na sledeći način:
za svaku usmerenu granu dužine t od čvora u do čvora v dodajemo:
d[1][(u, 0)][(v, t-1)] += 1.
Logika iza ovoga: Ako krenemo ovom granom, ostaće nam još t-1 da pređemo do čvora v.
Za svaku neusmerenu granu samo dodamo odgovarajuće dve usmerene.
Dodatno, za svaki čvor u i svako t od 1 do 9 dodajemo:
d[1][(u, t)][(u, t-1)] += 1.
Ako se trenutno nalazimo unutar neke grane, nakon što pređemo još 1 “metar” bićemo na istoj grani, na razdaljini t-1 ili ćemo biti baš u čvoru u, na razdaljini 0 (slučaj t=1).
Sada ovakvu matricu možemo prethodno opisanim postupkom možemo stepenovati i naći zbir odgovarajućih stepena.
Složenost ovog rešenja je O((n * Tmax)^3 * log K), što je uz manje optimizacije dovoljno da se dobije 100 poena.
